題目

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

Example 1:

Input: "babad"
Output: "bab"
Note: "aba" is also a valid answer.

Example 2:

Input: "cbbd"
Output: "bb"

在刷這題的時候居然卡了整整一個下午, 超慚愧…
搜了一下說明居然有O(N)的演算法真的是嚇死人了, 看了三天總算看懂了, 好丟臉QQ
趁還新鮮趕快紀錄起來!

Manacher’s Algorithm

基本概念

以string S 的每個char S[i] 為中心, 由左至右逐一計算Function Z(i), 將 Z(i) 存入陣列 LPS
接著取 LPS 中的最大值所在的index i, 答案就是以 i 為中心的字串 s’.

  • Z(i) : 以i為中心的最長對稱的子字串半徑
  • s’ = S[i - Z(i),…, i+Z(i)]
  • 例如: babab 之正中間b(index = 2), Z(2) = 2,s’ = S[2-2,…,2+2] -> babab

但是這沒辦法處理偶數長度如 abba 這種case,所以必須先將字串 S 處理過, 方法是

  • 在每個字的前後加上不會出現的字元 ‘#’, 處理後的字串長度為 2N + 1 例 : baab 變成 #b#a#a#b#

這個是 O(N^2), 因為每個點我們都必須往左右兩側loop找相等的字元.

基本版程式碼

int Z(string s, int l, int r){
  int ret = 0
  while(l >= 0 && r < s.length() && s[l] == s[r]){
    ret += 1;
    l -= 1;
    r += 1;
  }
  return ret;
}
string basic_manacher(string s) {
  // pre-process s
  string S = "#";
  for(int i = 0; i < s.length(); i++){
    S = S + s[i] + '#';
  }

  // calculate LPS array
  int *LPS = new int[S.length()];
  for(int i = 0; i < S.length(); i++){
    LPS[i] = Z(S, i - 1, i + 1);
  }

  // find the index of max LPS
  int max_Z = 0, max_center=0;
  for(int i = 0; i < S.length();i++){
    if(LPS[i] >= max_Z){
      max_Z = LPS[i];
      max_center = i;
    }
  }

  // get the sub string of S[max_center - max_Z, ..., max_center + max_Z] and remove "#"
  string ans;
  for(int i = max_center - max_Z ; i < max_center + max_Z; i++){
    if(S[i] == '#') 
      continue;
    ans += S[i];
  }
  return ans;
}

核心概念: 利用曾經算過的 Z 值與回文特性, 來減少計算接下來字元 Z 值的次數

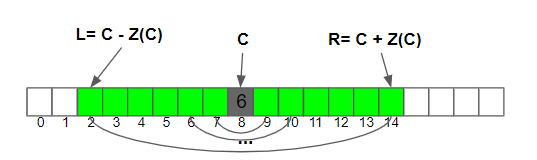
Basic_Concept

如圖, 假設目前已經計算出 Z(C) = 6, 這代表C開始的左右兩側六個字元兩兩相等, 得到以下結論 1
很像廢話但是很重要!! 因為我們要利用上述特性來省略接下來的Z(i)到Z(R)

1. S[7]=S[9], S[6]=S[10], S[5]=S[11], S[4] = S[12], ..., S[2]=S[14]

分以下3個Case說明

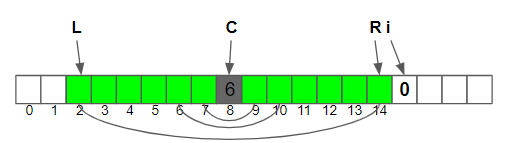
Case 1. i > R

Case 1

  • 初始狀況, 因為超出邊介, 得從頭開始算, Z(i) = 0

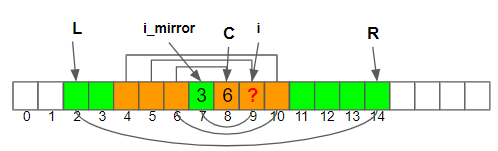
Case 2a. i < R && i + LPS[i_mirror] < R

Case 2a

  • 以C為中心, 找到 i=9 的對稱點, i_mirror = C - (i - C) = 7
  • Z(7) = 3, 可以導出 2
  • 用小學數學結合 1, 2, 得到結論 3
  • 那接下來的S[5]與S[13]是否相等? 答案是還是得重新計算!, 因為以現有的資訊只能推出Z(i)的起始值

2. S[7]=S[9], S[6]=S[10], S[5]=S[11], S[4] = S[12], …, S[2]=S[14]

3. S[8]=S[10], S[7] = S[11], S[6]=S[12] -> Z(i) = 3

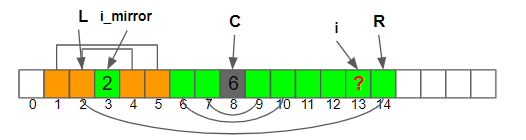
Case 2b. i < R && i + LPS[i_mirror] >= R

Case 2b

  • 當 i 已經或將會超出右邊邊界 R, 這時很明顯的我們沒有比對過, 所以需要重新計算Z值
  • Z(3) = 2, 得到 4
  • 結合 1與 4, 得到 5.
  • 甚至可以確定Z(13) = 1且不用再算接下來的Z, 因為如果 S[11] = S[15], 則 S[1]=S[15] , Z(8) = 7, != 6 不過這個會被接下來的判斷檢查到, 所以就不需要特別處理

4. S[2]=S[4], S[1]=S[5]

5. S[12]=S[14]

結論

結合Case 2a & Case 2b, 我們可以確定 Z(i) 的初始值為

Z(i) = min(LPS[i_mirror], R - i)

接著再利用Z(i)的初始值跳到沒比對的字 l , r開始比對, 省下往左右開始找的時間, 也就是一個Order!

完整版程式碼

int Z(string s, int begin_Z, int l, int r){
    while(l >= 0 && r < s.length() && s[l] == s[r]){
        begin_Z += 1;
        l -= 1;
        r += 1;
    }
    return begin_Z;
}

string manacher(string s) {
    // pre-process s
    string S = "#";
    for(int i = 0; i < s.length(); i++){
        S = S + s[i] + '#';
    }

    // allocate LPS array
    int *LPS = new int[S.length()];
    int C = 0, R = 0; // don't need L since we only need check i < R or i >= R
    int max_Z = 0;
    for(int i = 0; i < S.length(); i++){
        if(i >= R){
            // Case 1, need calculate Z from beginning
            LPS[i] = 0;
        }
        else{
            // Case 2a & 2b, get init value from LPS[i_mirror]
            int i_mirror = C - (i - C);
            LPS[i] = min(LPS[i_mirror], R - i);
        }
        // get first never calculated index
        int l = i - LPS[i] - 1;
        int r = i + LPS[i] + 1;
        LPS[i] = Z(S, LPS[i], l, r);

        // update C & R when we found new max Z
        if(LPS[i] > max_Z){
            max_Z = LPS[i];
            C = i;
            R = C + LPS[i];
        }
    }
    delete [] LPS;

    // get the sub string of S[C - max_Z, ..., C + max_Z] and remove "#"
    string ans;
    for(int i = C - max_Z ; i < C + max_Z; i++){
        if(S[i] == '#') continue;
        ans += S[i];
    }

    return ans;
}